"... y me llevo una" está bastante out. Cómo explicar restas con llevadas

Queridos papás que estudiasteis EGB: si teneis la suerte de tener un pequeñ@ de 2º de EP en casa, no desaprovecheis la ocasión: planteadle una resta con llevada y preguntadle cómo la resuelve. Vereis que estais más out que nuestras queridas Ángeles de Charlie (me encantaban las tres !!!)

Si su profe es de la vieja escuela, la cantinela de "me llevo una" os sonará familiar.

Pero el método actual para resolver restas con llevadas no es el que nos explicaron a nosotros. Ahora lo que se lleva, mucho más intuitivo y más lógico, es "este número le da una decena".

Para entender la diferencia entre los dos métodos pongamos un ejemplo, que vamos a resolver primero por el nuestro, al que llamaremos "me llevo una", y después por el suyo, que podemos llamar "este número le da una decena".

Esta inocente resta nos va a servir como ejemplo:

1.- Método "me llevo una" (nosotros la resolveríamos así): 

En la columna de las unidades, como el 7 es mayor que el 1, diríamos: "de 7 a 11 van 4 y me llevo una"

"de 7 a 11 van 4 y me llevo una"

En la columna de las decenas, ese 1 "que me llevo" se lo sumaríamos al 2 de abajo y diríamos: "2 más 1 que me llevaba son 3, y de 3 a 5 van 2"

"2 más 1 que me llevaba son 3, y de 3 a 5 van 2"

2.- Método "este número le da una decena" (ahora los niñ@s lo resuelven así):

En la columna de las unidades, como el 7 es mayor que el 1, el 1 le "pide prestada" una decena al 5, y el 5 se la "da":

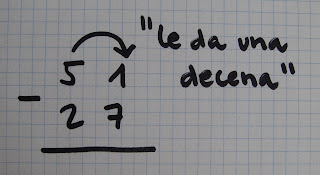El 5 le "da" una decena al 1

Al darle una decena, el 5 (que, como está en la columna de las decenas, vale 50 unidades), pasa a ser un 4, (o sea 40 unidades). Y el 1, al recibir esa decena, pasa a ser un 11. Queda por tanto una resta que sí se puede hacer directamente:

Ahora tenemos 4 decenas y 11 unidades, en lugar de 5 decenas y 1 unidad

Fijaos que todo se basa en plantear el número 51 de dos maneras distintas: 5 decenas + 1 unidad (lo que da lugar a "me llevo una") o 4 decenas + 11 unidades (de esta manera no te "llevas" nada a ningún sitio):

¿Qué método te parece más intuitivo? Para mi gusto, un gran avance en el cálculo más básico. 

¡¡¡SUPERFÁCIL Y SIN RECETAS!!!

Cálculo de Raíces Cuadradas (a mano)

Hoy la entrada va dedicada a mi sobrina Leire, una niña muy responsable de 6º de EP, que me dijo el otro día que en el cole estaba aprendiendo a calcular raíces cuadradas. Yo creía que esa operación ya estaba desterrada del temario de Matemáticas, (de hecho yo no la encuentro en los currículos oficiales, ¿alguien sabe si aparece en algún sitio?), pero ya veo que no, al menos no del todo.

A falta de calculadora, yo veo más intuitivo el cálculo de raíces por aproximaciones sucesivas, que tiene la ventaja de que no hay que recordar cómo se hacen las dichosas raíces cuadradas, y que, además, es un método que se puede hacer extensivo para raíces cúbicas o de cualquier otro índice.

En fin, lo prometido es deuda. Querida Leire, espero que te sirva de ayuda (a ti y a tu madre, que tuvo que buscar en internet cómo se hacían. Porque... ¿cuántos de los que estudiamos EGB podríamos hacer una raíz sin "chuleta"?)

• Lo primero que hay que saber es que calcular la raíz cuadrada de un número (radicando) es buscar otro número (raíz) que al multiplicarlo por sí mismo nos devuelva el primer número. Es decir:

• Si sólo manejamos números enteros, lo que pone en la imagen anterior sólo es posible cuando el radicando sea un cuadrado perfecto. Si el radicando no es un cuadrado perfecto, al hacer la raíz obtendremos un resto, (algo que sobra al final), y la cosa quedará así:

• Si trabajamos con números decimales, podremos seguir calculando cifras decimales de la raíz hasta que encontremos un resultado exacto, o, si no lo encontramos, todas las que queramos (esto lo veremos en otro post)

• Empiezo con un ejemplo cortito del cálculo de una raíz exacta (pido disculpas por el vídeo, bastante amateur, habrá que ir mejorando esto con el tiempo):

• Otro ejemplo más de raíz exacta, esta vez un poquito más largo:

• Y, como ejemplo de cálculo de raíz no exacta, te dejo esta imagen, para ver si sabes reproducir el cálculo. El procedimiento es el mismo de los dos ejemplos anteriores, pero ahora en la última resta, obtenemos un número distinto de cero. Ese número se llama resto, y es lo que le falta al cuadrado de la raíz para igualar al radicando:

¡ BUEN CÁLCULO !