 Todas las fracciones se pueden escribir en forma de número decimal.
Todas las fracciones se pueden escribir en forma de número decimal.Sólo hay que dividir el numerador entre el denominador. Si lo hacemos, veremos que nos pueden pasar varias cosas:
- El resultado puede ser un número entero:
- puede ser un decimal exacto:
- o un decimal periódico:
Pero, ¡ojo!, no todos los números decimales se pueden escribir en forma de fracción. Sólo podemos escribir en forma de fracción los decimales exactos y los decimales periódicos (ya veremos en otro post cuáles no y porqué). Veamos algunos ejemplos:
- Cuando el decimal es exacto el procedimiento es muy fácil, gracias a nuestro sistema decimal de numeración:
(fíjate que en el segundo ejemplo, hemos "reducido" la fracción dividiendo el numerador y el denominador entre 2, hasta llegar a la fracción irreducible). A estas fracciones que obtenemos se les llama fracción generatriz de un número decimal.
- Cuando el decimal es periódico no es tan obvio a simple vista, pero fíjate qué fácil es si nos quitamos el periodo de encima mediante el siguiente procedimiento:
Vamos a expresar como fracción el número
Para que se entienda bien lo que vamos a hacer con este número, vamos a llamarlo "x":
Vamos a multiplicar el número por 10, de forma que "pasamos" un 4 del periodo a la parte entera:
Y ahora restamos las dos ecuaciones anteriores:
Y ya sólo falta despejar "x" de esta ecuación tan fácil:
¡¡¡LO HEMOS CONSEGUIDO!!!
- Y... ¡más difícil todavía! Cuando el número decimal tiene anteperiodo (así se llaman las cifras decimales que no se repiten y que van antes del periodo), el procedimiento tiene un pasito más. Otro ejemplo:
Ahora vamos a calcular la fracción generatriz del número
y, como antes, lo vamos a llamar "x":
Lo multiplicamos por 10 para "pasar" la cifra del anteperiodo a la parte entera:
Y lo multiplicamos por 100 para "pasar" la cifra del periodo a la parte entera:
Restamos las dos ecuaciones anteriores:
Y sólo queda despejar la "x" de esta ecuación tan facilona:
(fíjate que, siempre que sea posible, la fracción obtenida se "reduce" hasta su fracción irreducible)
¡¡¡ CONSEGUIDO !!!
Si te vas a poner a hacer ejercicios y quieres comprobar tus resultados, puedes usar el generador de fracciones generatriz del blog NoSoloMates. Pincha aquí.
Si has llegado hasta aquí, ¿por qué no pruebas algo que te va a sorprender?
Trata de calcular la fracción generatriz de 0,99999..... y comprobarás que:
¿Curioso, verdad?
Si quieres otra demostración, con anécdota incluida, pincha aquí.
¡BUEN CÁLCULO!

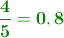

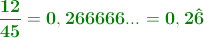
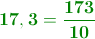





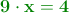









me gusto aprendi mejor gracias
ResponderEliminarLogre entender!! Gracias!
ResponderEliminares tu culo
ResponderEliminar